by A. Pomberger, N. Jose, D. Walz, J. Meissner, C. Holze, M. Kopczynski, P. Müller-Bischof, A.A. Lapkin
Abstract
Buffer solutions have tremendous importance in biological systems and in formulated products. Whilst the pH response upon acid/base addition to a mixture containing a single buffer can be described by the Henderson-Hasselbalch equation, modelling the pH response for multi-buffered poly-protic systems after acid/base addition, a common task in all chemical laboratories and many industrial plants, is a challenge. Combining predictive modelling and experimental pH adjustment, we present an active machine learning (ML)-driven closed-loop optimization strategy for automating small scale batch pH adjustment relevant for complex samples (e.g., formulated products in the chemical industry). Several ML models were compared on a generated dataset of binary-buffered poly-protic systems and it was found that Gaussian processes (GP) served as the best performing models. Moreover, the implementation of transfer learning into the optimization protocol proved to be a successful strategy in making the process even more efficient. Finally, practical usability of the developed algorithm was demonstrated experimentally with a liquid handling robot where the pH of different buffered systems was adjusted, offering a versatile and efficient strategy for a pH adjustment processes.
Graphical Abstract
Introduction
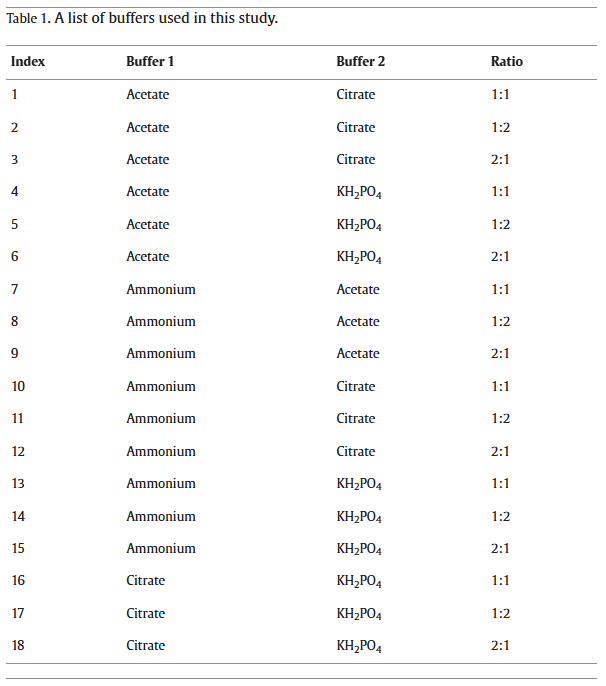
Materials and methods
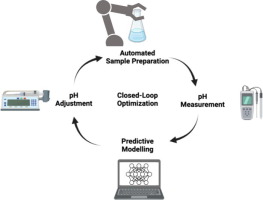
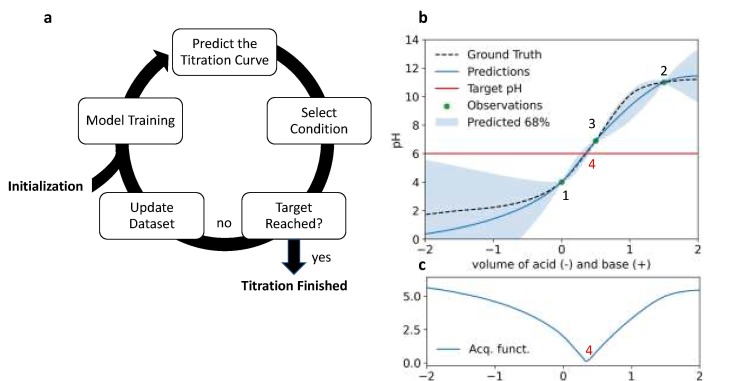
Active ML-driven closed-loop optimization

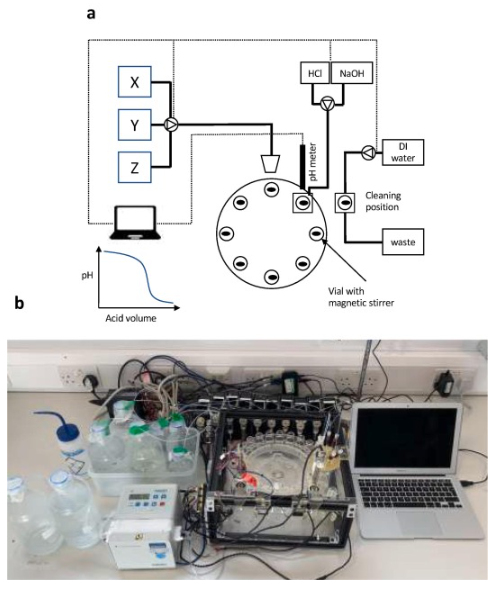
Robotic platform
Results and discussion
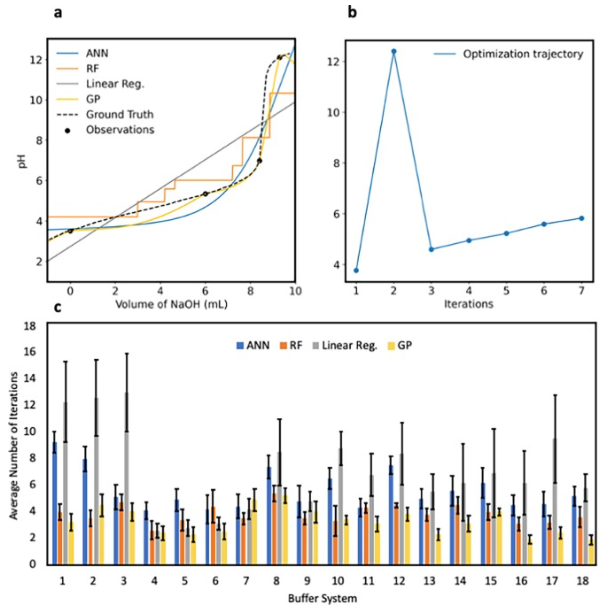
Closed-loop optimization pH-adjustment
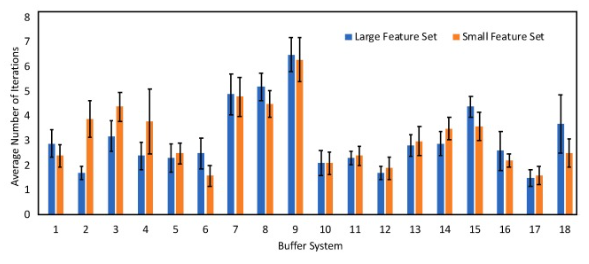
Featurization effects
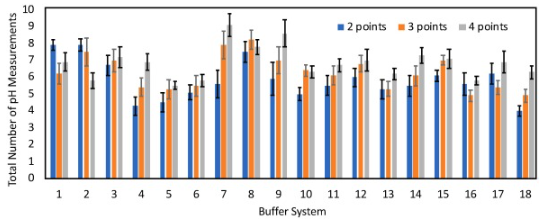
Variation of the number of datapoints for model initialization
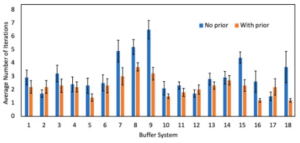
Transfer learning-accelerated closed-loop optimization
Real-time automated pH adjustment
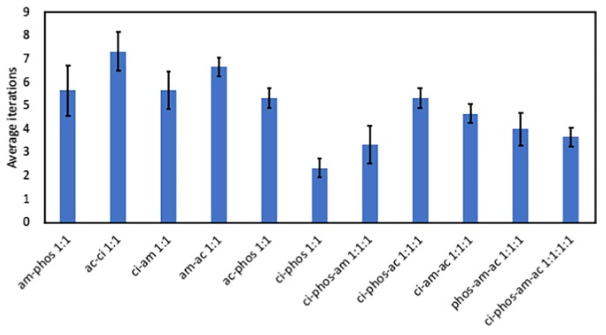
Conclusions
Declaration of Competing Interest
Acknowledgments
Authors contributions
Appendix A. Supplementary data
The following are the Supplementary data to this article:Supplementary data 1.
References
-
Evidence-based guidelines for controlling pH in mammalian live-cell culture systemsCommun. Biol., 2 (1) (2019), p. 144
-
pH-Control problems of wastewater treatment plantsAl-Khwarizmi Eng. J., 4 (2) (2008), pp. 37-45
-
R.K. Goel, J.R.V. Flora, J.P. Chen, Flow Equalization and Neutralization. In Physicochemical Treatment Processes. Handbook of Environmental Engineering, 2005; Vol. 3, pp 22-26.
-
Towards optimal pH of the skin and topical formulations: from the current state of the art to tailored productsCosmetics, 8 (3) (2021), p. 69
-
Role of pH in skin cleansingInt. J. Cosmet. Sci., 43 (4) (2021), pp. 474-483
-
Improvement of washing properties of liquid laundry detergents by modification with N-hexadecyl-N, N-dimethyl-3-ammonio-1-propanesulfonate sulfobetaineText. Res. J., 91 (1–2) (2020), pp. 115-129
-
Modeling and control of a pilot pH plant using genetic algorithmEng. Appl. Artif. Intell., 18 (4) (2005), pp. 485-494
-
Die Berechnung der Wasserstoffzahl des Blutes aus der freien und gebundenen Kohlensaeuure desselben, und die Sauerstoffbindung des Blutes als Funktion der WasserstoffzahlBiochemische Zeit, 78 (1916), pp. 112-144
-
Calculation of the equilibrium pH in a multiple-buffered aqueous solution based on partitioning of proton buffering: a new predictive formulaAm. J. Physiol.-Renal Physiol., 296 (6) (2009), pp. F1521-F1529
-
A brief history of automatic controlIEEE Control Syst. Mag., 16 (3) (1996), pp. 17-25
-
Development of an automatic pH adjustment instrument for the preparation of analytical samples prior to solid phase extractionAnal. Sci., 36 (5) (2020), pp. 621-626
-
Bioreactor profile control by a nonlinear auto regressive moving average neuro and two degree of freedom PID controllersJ. Process Control, 24 (11) (2014), pp. 1761-1777
-
PID controls: the forgotten bioprocess parametersDiscover Chemical Engineering, 2 (1) (2022), pp. 1-18
-
V. Chotteau, H. Hjalmarsson, In Tuning of Dissolved Oxygen and pH PID Control Parameters in Large Scale Bioreactor by Lag Control, Proceedings of the 21st Annual Meeting of the European Society for Animal Cell Technology (ESACT), , 2009; pp 327-330.
-
Effective bioreactor pH control using only sparging gasesBiotechnol. Prog., 35 (1) (2019), pp. 1-7
-
Generalized predictive control applied to a pH neutralization processComput. Chem. Eng., 31 (10) (2007), pp. 1199-1204
-
H. Helmy, D.A.M. Janah, A. Nursyahid, M.N. Mara, T.A. Setyawan, A.S. Nugroho, In Nutrient Solution Acidity Control System on NFT-Based Hydroponic Plants Using Multiple Linear Regression Method, 2020 7th International Conference on Information Technology, Computer, and Electrical Engineering (ICITACEE), pp 272-276.
-
Learning From Experience: An Automatic pH Neutralization System Using Hybrid Fuzzy System and Neural NetworkProcedia Comput. Sci., 140 (2018), pp. 206-215
-
An improved approach for robust MPC tuning based on machine learningMathematical Problems in Engineering, 2021 (2021), pp. 1-18
-
Neural network approximation of a nonlinear model predictive controller applied to a pH neutralization processComput. Chem. Eng., 29 (2) (2005), pp. 323-335
-
A Survey on Transfer LearningIEEE Trans. Knowl. Data Eng., 22 (2010), pp. 1345-1359
-
Transfer learning enables the molecular transformer to predict regio- and stereoselective reactions on carbohydratesNat. Commun., 11 (1) (2020), pp. 1-8
-
Data augmentation and transfer learning strategies for reaction prediction in low chemical data regimesOrg. Chem. Front., 8 (7) (2021), pp. 1415-1423
-
Machine learning and molecular descriptors enable rational solvent selection in asymmetric catalysisChem. Sci., 10 (27) (2019), pp. 6697-6706
-
Solvent selection for Mitsunobu reaction driven by an active learning surrogate modelOrg. Process Res. Dev., 24 (12) (2020), pp. 2864-2873
-
M. Mohri, A. Rostamizadeh, A. Talwalkar, Foundations of machine learning. MIT press: 2012.
-
Machine learning: Trends, perspectives, and prospectsScience, 349 (6245) (2015), pp. 255-260
-
Machine learning and the physical sciencesRev. Mod. Phys., 91 (4) (2019), pp. 1-39
-
Iterative experimental design based on active machine learning reduces the experimental burden associated with reaction screeningReact. Chem. Eng., 5 (10) (2020), pp. 1963-1972
-
Multi-objective Bayesian optimisation of a two-step synthesis of p-cymene from crude sulphate turpentineChem. Eng. Sci., 116938 (2021), pp. 1-10
-
Bayesian reaction optimization as a tool for chemical synthesisNature, 590 (7844) (2021), pp. 89-96
-
T.K. Ho, Random decision forests. Proceedings of 3rd International Conference on Document Analysis and Recognition 1995, 1, 278-282.
-
Gaussian Processes for Machine LearningMIT Press (2006)
-
Deep learning in neural networks: an overviewNeural Networks, 61 (2015), pp. 85-117
-
L. Cao, D. Russo, K. Felton, D. Salley, A. Sharma, G. Keenan, W. Mauer, H. Gao, L. Cronin, A.A. Lapkin, Optimization of Formulations Using Robotic Experiments Driven by Machine Learning DoE. Cell Reports Physical Science 2021, 2 (1), 100295 1-17.
- [36]
A Modular Programmable Inorganic Cluster Discovery Robot for the Discovery and Synthesis of PolyoxometalatesACS Cent. Sci., 6 (9) (2020), pp. 1587-1593
-
Nicolas, J. FLab. https://pypi.org/project/flab/ (accessed 23.04.22).
-
Regression trees with unbiased variable selection and interaction detectionStatistica Sinica, 12 (2002), pp. 361-386
- D.S. Wigh, J.M. Goodman, A.A. Lapkin
A review of molecular representation in the age of machine learningWIREs Comput. Mol. Sci., e1603 (2022), pp. 1-19
- A. Pomberger, A.A. Pedrina McCarthy, A. Khan, S. Sung, C.J. Taylor, M.J. Gaunt, L. Colwell, D. Walz, A.A. Lapkin
The effect of chemical representation on active machine learning towards closed-loop optimizationReact. Chem. Eng., 7 (2022), pp. 1368-1379
This article is cited by